How Many Random Seeds ?

Reproducibility in Machine Learning and Deep Reinforcement Learning in particular has become a serious issue in the recent years. Reproducing an RL paper can turn out to be much more complicated than you thought, see this blog post about lessons learned from reproducing a deep RL paper. Indeed, codebases are not always released and scientific papers often omit parts of the implementation tricks. Recently, Henderson et al. conducted a thorough investigation of various parameters causing this reproducibility crisis [Henderson et al., 2017]. They used trendy deep RL algorithms such as DDPG, ACKTR, TRPO and PPO with OpenAI Gym popular benchmarks such as Half-Cheetah, Hopper and Swimmer to study the effects of the codebase, the size of the networks, the activation function, the reward scaling or the random seeds. Among other results, they showed that different implementations of the same algorithm with the same set of hyperparameters led to drastically different results.

Perhaps the most surprising thing is this: running the same algorithm 10 times with the same hyper-parameters using 10 different random seeds and averaging performance over two splits of 5 seeds can lead to learning curves seemingly coming from different statistical distributions. Then, they present this table:

_{Figure 1: Number of trials reported during evaluation in various works, from [Henderson et al., 2017].}

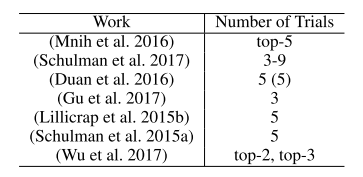
This table shows that all the deep RL papers reviewed by Henderson et al. use less than 5 seeds. Even worse, some papers actually report the average of the best performing runs! As demonstrated in Henderson et al., these methodologies can lead to claim that two algorithms performances are different when they are not. A solution to this problem is to use more random seeds, to average more different trials to obtain a more robust measure of your algorithm performance. OK, but how many more? Should I use 10, should I use 100 as in [Mania et al, 2018]? The answer is, of course, it depends.

If you read this blog, you must be in the following situation: you want to compare the performance of two algorithms to determine which one performs best in a given environment. Unfortunately, two runs of the same algorithm often yield different measures of performance. This might be due to various factors such as the seed of the random generators (called random seed or seed thereafter), the initial conditions of the agent, the stochasticity of the environment, etc.

Part of the statistical procedures described in this article are available on Github here. The article is available on ArXiv here.

Definition of the statistical problem

The performance of an algorithm can be modeled as a random variable \(X\) and running this algorithm in an environment results in a realization \(x\). Repeating the procedure \(N\) times, you obtain a statistical sample \(x=(x^1, .., x^N)\). A random variable is usually characterized by its mean \(\mu\) and its standard deviation, noted \(\sigma\). Of course, you do not know what are the values of \(\mu\) and \(\sigma\). The only thing you can do is to compute their estimations \(\overline{x}\) and \(s\):

where \(\overline{x}\) is called the empirical mean, and \(s\) is called the empirical standard deviation. The larger the sample size \(N\), the more confidence you can be in the estimations.

Here, two algorithms with respective performances \(X_1\) and \(X_2\) are compared. If \(X_1\) and \(X_2\) follow normal distributions, the random variable describing their difference \((X_{\text{diff}} = X_1-X_2)\) also follows a normal distribution with parameters \({\sigma_{diff}=(\sigma_1^2+\sigma_2^2)^{1/2}}\) and \(\mu_{\text{diff}}=\mu_1-\mu_2\). In this case, the estimator of the mean of \(X_{\text{diff}}\) is \(\overline{x}_{\text{diff}} = \overline{x}_1-\overline{x}_2\) and the estimator of \({\sigma_{\text{diff}}}\) is \({s_{\text{diff}}=\sqrt{s_1^2+s_2^2}}\). The effect size \(\epsilon\) can be defined as the difference between the mean performances of both algorithms: \({\epsilon = \mu_1-\mu_2}\).

Testing for a difference between the performances of two algorithms ( \(\mu_1\) and \(\mu_2\)) is mathematically equivalent to testing a difference between their difference \(\mu_{\text{diff}}\) and 0. The second point of view is considered from now on. We draw a sample \(x_{\text{diff}}\) from \(X_{\text{diff}}\) by subtracting two samples \(x_1\) and \(x_2\) obtained from \(X_1\) and \(X_2\).

Example 1

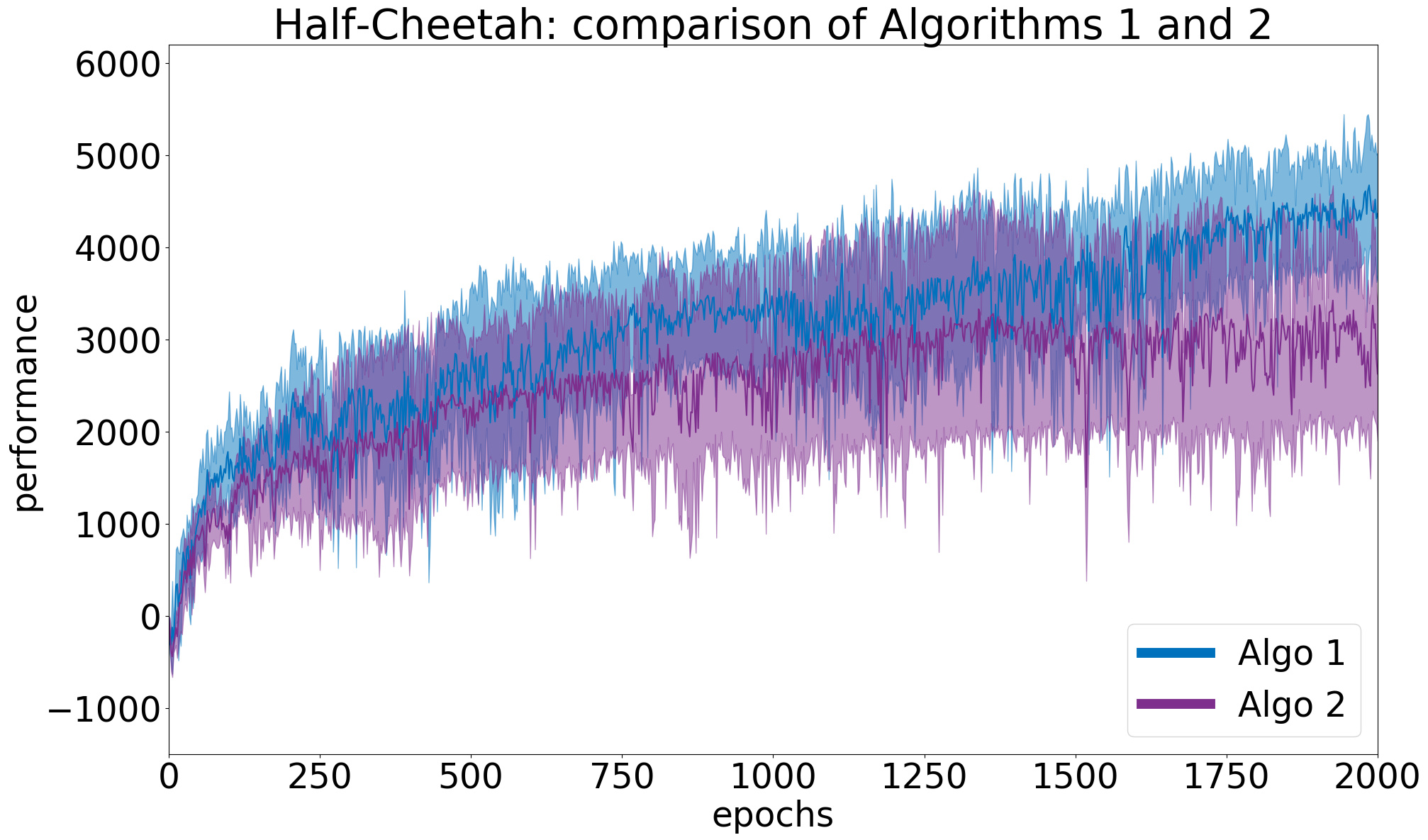
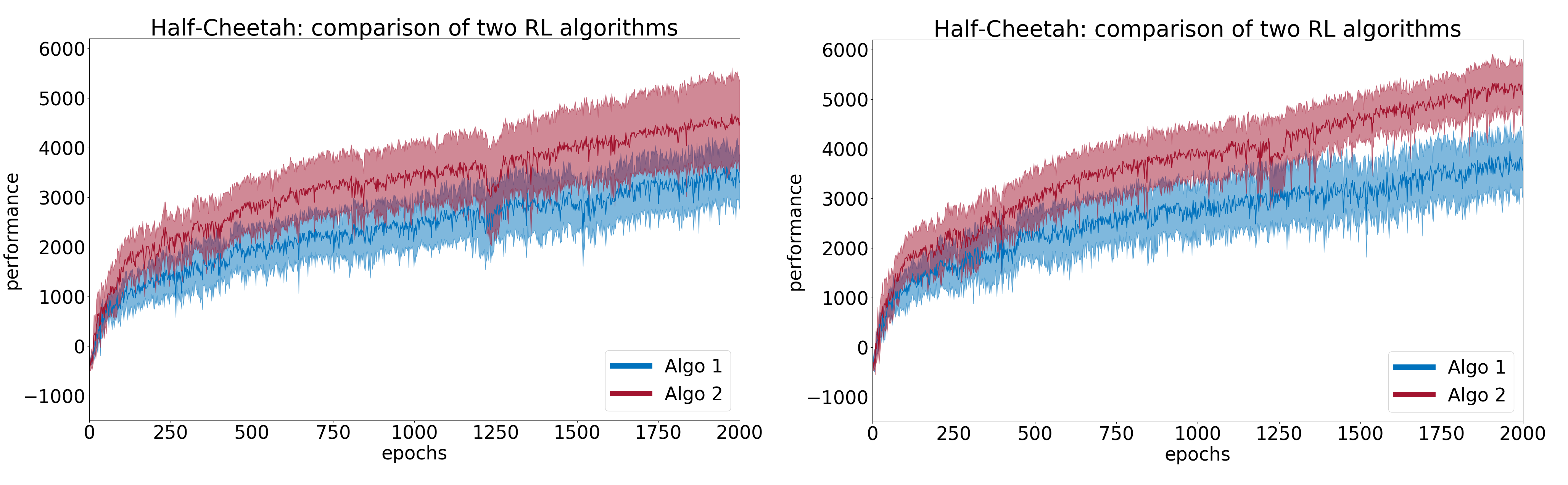
To illustrate the concepts developed in this article, let us take two algorithms (\(Algo 1\) and \(Algo 2\)) and compare them on the Half-Cheetah environment from the OpenAI Gym framework. The actual algorithms used are not so important here, and will be revealed later. First, we run a preliminary study with \(N=5\) random seeds for each and plot the results in Figure 2. This figure shows the average learning curves, with the \(95\%\) confidence interval. Each point of a learning curve is the average cumulated reward over \(10\) evaluation episodes. The measure of performance of an algorithm is the average performance over the last \(10\) points (i.e. last \(100\) evaluation episodes). From the figure, it seems that \(Algo1\) performs better than \(Algo2\). Moreover, the confidence intervals do not overlap much at the end. Of course, we need to run statistical tests before drawing any conclusion.

_{Figure 2: Algo1 versus Algo2 on Half-Cheetah. Mean and confidence intervals for 5 seeds}

</div>

Comparing performances with a difference test

In a difference test, statisticians define the null hypothesis \(H_0\) and the alternate hypothesis \(H_a\). \(H_0\) assumes no difference whereas \(H_a\) assumes one:

• \(H_0\): \(\mu_{\text{diff}} = 0\)
• \(H_a\): \(\mu_{\text{diff}} \neq 0\)

These hypothesis refers to the two-tail case. When you have an a-priori on which algorithm performs best, (let us say \(Algo1\)), you can use the one-tail version:

• \(H_0\): \(\mu_{\text{diff}} \leq 0\)
• \(H_a\): \(\mu_{\text{diff}} > 0\)

At first, a statistical test always assumes the null hypothesis. Once a sample \(x_{\text{diff}}\) is collected from \(X_{\text{diff}}\), you can estimate the probability \(p\) (called \(p\)-value) of observing data as extreme, under the null hypothesis assumption. By extreme, one means far from the null hypothesis (\(\overline{x}_{\text{diff}}\) far from \(0\)). The \(p\)-value answers the following question: how probable is it to observe this sample or a more extreme one, given that there is no true difference in the performances of both algorithms? Mathematically, we can write it this way for the one-tail case:

and this way for the two-tail case:

When this probability becomes really low, it means that it is highly improbable that two algorithms with no performance difference produced the collected sample \(x_{\text{diff}}\). A difference is called significant at significance level \(\alpha\) when the \(p\)-value is lower than \(\alpha\) in the one-tail case, and lower than \(\alpha/2\) in the two tail case to account for the two sided test. Usually \(\alpha\) is set to \(0.05\) or lower. In this case, the low probability to observe the collected sample under hypothesis \(H_0\) results in its rejection. Note that a significance level \(\alpha=0.05\) still results in \(1\) chance out of \(20\) to claim a false positive, to claim that there is a true difference when there is not.

Another way to see this, is to consider confidence intervals. Two kinds of confidence intervals can be computed:

• \(CI_1\): The \(100\cdot(1-\alpha)\%\) confidence interval for the mean of the difference \(\mu_{\text{diff}}\) given a sample \(x_{\text{diff}}\) characterized by \(\overline{x}_{\text{diff}}\) and \(s_{\text{diff}}\).
• \(CI_2\): The \(100\cdot(1-\alpha)\%\) confidence interval for any realization of \(X_{\text{diff}}\) under \(H_0\) (assuming \(\mu_{\text{diff}}=0\)).

Having \(CI_2\) that does not include \(\overline{x}_{\text{diff}}\) is mathematically equivalent to a \(p\)-value below \(\alpha\). In both cases, it means there is less than \(100\cdot\alpha\%\) chance that \(\mu_{\text{diff}}=0\) under \(H_0\). When \(CI_1\) does not include \(0\), we are also \(100\cdot(1-\alpha)\%\) confident that \(\mu\neq0\), without assuming \(H_0\). Proving one of these things leads to conclude that the difference is significant at level \(\alpha\).

Two types of errors can be made in statistics:

• The type-I error rejects \(H_0\) when it is true, also called false positive. This corresponds to claiming the superiority of an algorithm over another when there is no true difference. Note that we call both the significance level and the probability of type-I error \(\alpha\) because they both refer to the same concept. Choosing a significance level of \(\alpha\) enforces a probability of type-I error \(\alpha\), under the assumptions of the statistical test.
• The type-II error fails to reject \(H_0\) when it is false, also called false negative. This corresponds to missing the opportunity to publish an article when there was actually something to be found.

Important:

• \(H_0\): \(\mu_{\text{diff}} \leq 0\)
• \(H_a\): \(\mu_{\text{diff}} > 0\)
• In the two-tail case, the null hypothesis \(H_0\) is \(\mu_{\text{diff}}=0\). The alternative hypothesis \(H_a\) is \(\mu_{\text{diff}}\neq0\)
• \(p\)-value \(=P(X_{\text{diff}}\geq \overline{x}_{\text{diff}} \mid H_0)\).
• A difference is said statistically significant when a statistical test passed. One can reject the null hypothesis when 1) \(p\)-value \(<\alpha\); 2) \(CI_1\) does not contain \(0\); 3) \(CI_2\) does not contain \(\overline{x}_{\text{diff}}\).
• statistically significant does not refer to the absolute truth. Two types of error can occur. Type-I error rejects \(H_0\) when it is true. Type-II error fails to reject \(H_0\) when it is false. \(x\)

Select the appropriate statistical test

You must decide which statistical tests to use in order to assess whether the performance difference is significant or not. As recommended in [Henderson et al., 2017], the two-sample t-test and the bootstrap confidence interval test can be used for this purpose. Henderson et al. also advised for the Kolmogorov-Smirnov test, which tests if two samples comes from the same distribution. This test should not be used to compare RL algorithms because it is unable to prove any order relation.

T-test and Welch’s t-test

We want to test the hypothesis that two populations have equal means (null hypothesis \(H_0\)). A 2-sample t-test can be used when the variances of both populations (both algorithms) are assumed equal. However, this assumption rarely holds when comparing two different algorithms (e.g. DDPG vs TRPO). In this case, an adaptation of the 2-sample t-test for unequal variances called Welch’s \(t\)-test should be used. \(T\)-tests make a few assumptions:

• The scale of data measurements must be continuous and ordinal (can be ranked). This is the case in RL.
• Data is obtained by collecting a representative sample from the population. This seem reasonable in RL.
• Measurements are independent from one another. This seems reasonable in RL.
• Data is normally-distributed, or at least bell-shaped. The normal law being a mathematical concept involving infinity, nothing is ever perfectly normally distributed. Moreover, measurements of algorithm performances might follow multi-modal distributions.

Under these assumptions, one can compute the \(t\)-statistic \(t\) and the degree of freedom \(\nu\) for the Welch’s \(t\)-test as estimated by the Welch–Satterthwaite equation, such as:

with \(x_{\text{diff}} = x_1-x_2\); \(s_1, s_2\) the empirical standard deviations of the two samples, and \(N\) the sample size (same for both algorithms). The \(t\)-statistics are assumed to follow a \(t\)-distribution, which is bell-shaped and whose width depends on the degree of freedom. The higher this degree, the thinner the distribution.

Figure 3 helps making sense of these concepts. It represents the distribution of the \(t\)-statistics corresponding to \(X_{\text{diff}}\), under \(H_0\) (left distribution) and under \(H_a\) (right distribution). \(H_0\) assumes \(\mu_{\text{diff}}=0\), the distribution is therefore centered on 0. \(H_a\) assumes a (positive) difference \(\mu_{\text{diff}}=\epsilon\), the distribution is therefore shifted by the \(t\)-value corresponding to \(\epsilon\), \(t_\epsilon\). Note that we consider the one-tail case here, and test for a positive difference.

A \(t\)-distribution is defined by its probability density function\(T_{distrib}^{\nu}(\tau)\) (left curve in Figure 3, which is parameterized by \(\nu\). The cumulative distribution function \(CDF_{H_0}(t)\) is the function evaluating the area under \(T_{distrib}^{\nu}(t)\) from \(\tau=-\infty\) to \(\tau=t\). This allows to write:

_{Figure 3: Representation of H0 and Ha under the t-test assumptions. Areas under the distributions represented in red, dark blue and light blue correspond to the probability of type-I error alpha, type-II error beta and the statistical power 1-beta respectively.}

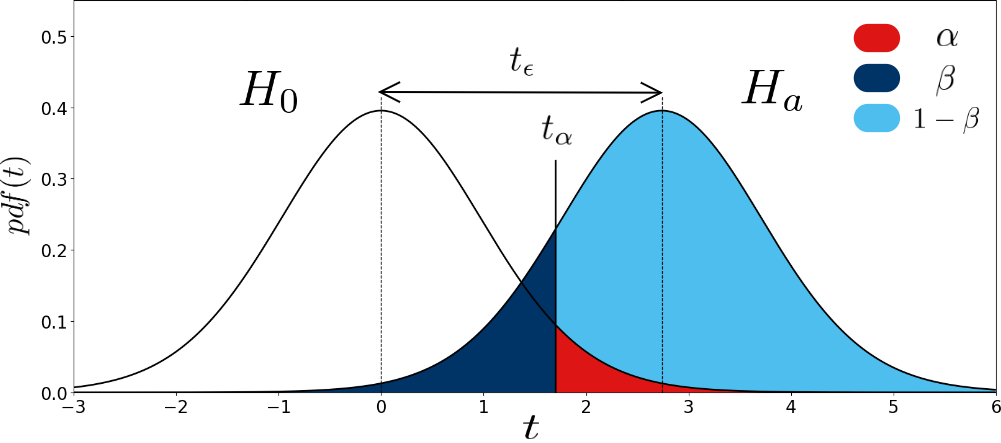
In Figure 3, \(t_\alpha\) represents the critical \(t\)-value to satisfy the significance level \(\alpha\) in the one-tail case. When \(t=t_\alpha\), \(p\)-value \(=\alpha\). When \(t>t_\alpha\), the \(p\)-value is lower than \(\alpha\) and the test rejects \(H_0\). On the other hand, when \(t\) is lower than \(t_\alpha\), the \(p\)-value is superior to \(\alpha\) and the test fails to reject \(H_0\). As can be seen in the figure, setting the threshold at \(t_\alpha\) might also cause an error of type-II. The rate of this error (\(\beta\)) is represented by the dark blue area: under the hypothesis of a true difference \(\epsilon\) (under \(H_a\), right distribution), we fail to reject \(H_0\) when \(t\) is inferior to \(t_\alpha\). \(\beta\) can therefore be computed mathematically using the \(CDF\):

\(\beta = CDF_{H_a}(t_\alpha) = \int_{-\infty}^{t_\alpha} T_{distrib}^{\nu}(\tau-t_{\epsilon}) \cdot d\tau.\) Using the translation properties of integrals, we can rewrite \(\beta\) as:

The procedure to run a Welch’s \(t\)-test given two samples \((x_1, x_2)\) is:

• Computing the degree of freedom \(\nu\) and the \(t\)-statistic \(t\) based on \(s_1\), \(s_2\), \(N\) and \(\overline{x}_{\text{diff}}\).
• Looking up the \(t_\alpha\) value for the degree of freedom \(\nu\) in a t-table or by evaluating the inverse of the \(CDF\) function in \(\alpha\).
• Compare the \(t\)-statistic to \(t_\alpha\). The difference is said statistically significant (\(H_0\) rejected) at level \(\alpha\) when \(t\geq t_\alpha\).

Note that \(t<t_\alpha\) does not mean there is no difference between the performances of both algorithms. It only means there is not enough evidence to prove its existence with \(100 \cdot (1-\alpha)\%\) confidence (it might be a type-II error). Noise might hinder the ability of the test to detect the difference. In this case, increasing the sample size \(N\) could help uncover the difference.

Selecting the significance level \(\alpha\) of the \(t\)-test enforces the probability of type-I error to \(\alpha\). However, Figure 3 shows that decreasing this probability boils down to increasing \(t_\alpha\), which in turn increases the probability of type-II error \(\beta\). One can decrease \(\beta\) while keeping \(\alpha\) constant by increasing the sample size \(N\). This way, the estimation \(\overline{x}_{\text{diff}}\) of \(\overline{\mu}_{\text{diff}}\) gets more accurate, which translates in thinner distributions in the figure, resulting in a smaller \(\beta\). The next section gives standard guidelines to select \(N\) so as to meet requirements for both \(\alpha\) and \(\beta\).

Bootstrapped confidence intervals

Bootstrapped confidence interval is a method that does not make any assumption on the distributions of performance differences. It estimates the confidence intervals by re-sampling among the samples actually collected and by computing the mean of each generated sample.

Given the true mean \(\mu\) and standard deviation \(\sigma\) of a normal distribution, a simple formula gives the \(95\%\) confidence interval. But here, we consider an unknown distribution \(F\) (the distribution of performances for a given algorithm). As we saw above, the empirical mean \(\overline{x}\) is an unbiased estimate of its true mean, but how do we compute a confidence interval? One solution is to use the bootstrap principle.

Let us say we have a sample \(x_1, x_2, .., x_N\) of measures (performance measures in our case), where \(N\) is the sample size. The empirical bootstrap sample is obtained by sampling with replacement inside the original sample. This bootstrap sample is noted \(x^*_1, x^*_2, …, x^*_N\) and has the same number of measurements \(N\). The bootstrap principle then says that, for any statistics \(u\) computed on the original sample and \(u^*\) computed on the bootstrap sample, variations in \(u\) are well approximated by variations in \(u^*\). More explanations and justifications can be found in this document from MIT. You can therefore approximate variations of the empirical mean (let’s say its range), by variations of the bootstrapped samples.

The computation would look like this:

• Generate \(B\) bootstrap samples of size \(N\) from the original sample \(x_1\) of \(Algo1\) and \(B\) samples from from the original sample \(x_2\) of \(Algo2\).
• Compute the empirical mean for each sample: \(\mu^1_1, \mu^2_1, ..., \mu^B_1\) and \(\mu^1_2, \mu^2_2, ..., \mu^B_2\)
• Compute the differences \(\mu_{\text{diff}}^{1:B} = \mu_1^{1:B}-\mu_2^{1:B}\)
• Compute the bootstrapped confidence interval at \(100\cdot(1-\alpha)\%\). This is basically the range between the \(100 \cdot\alpha/2\) and \(100\cdot(1-\alpha)/2\) percentiles of the vector \(\mu_{\text{diff}}^{1:B}\) (e.g. for \(\alpha=0.05\), the range between the \(2.5^{th}\) and the \(97.5^{th}\) percentiles).

The number of bootstrap samples \(B\) should be chosen large (e.g. \(>1000\)). If the confidence interval bounds does not contain \(0\), it means that you are confident at \(100 \cdot (1-\alpha)\)% that the difference is either positive (both bounds positive) or negative (both bounds negative). You just found a statistically significant difference between the performances of your two algorithms. You can find a nice implementation of this here.

Example 1 (continued) Here, the type-I error requirement is set to \(\alpha=0.05\). Running the Welch’s \(t\)-test and the bootstrap confidence interval test with two samples \((x_1,x_2)\) of \(5\) seeds each leads to a \(p\)-value of \(0.031\) and a bootstrap confidence interval such that \(P\big(\mu_{\text{diff}} \in [259, 1564]\big) = 0.05\). Since the \(p\)-value is below the significance level \(\alpha\) and the \(CI_1\) confidence interval does not include \(0\), both test passed. This means both tests found a significant difference between the performances of \(Algo1\) and \(Algo2\) with a \(95\%\) confidence. There should have been only \(5\%\) chance to conclude a significant difference if it did not exist. In fact, we did encounter a type-I error. I know that for sure because:

They are both the canonical implementation of DDPG [Lillicrap et al., 2015]. The codebase can be found on this repository. This means that \(H_0\) was the true hypothesis, there is no possible difference in the true means of the two algorithms. Our first conclusion was wrong, we committed a type-I error, rejecting \(H_0\) when it was true. In our case, we selected the two tests so as to set the type-I error probability \(\alpha\) to \(5\%\). However, statistical tests often make assumptions, which results in wrong estimations of the probability of the type-I error. We will see in the last section that the false positive rate was strongly under-evaluated.

Important:

• \(T\)-tests assume \(t\)-distributions of the \(t\)-values. Under some assumptions, they can compute analytically the \(p\)-value and the confidence interval \(CI_2\) at level \(\alpha\).
• The Welch’s \(t\)-test does not assume both algorithms have equal variances but the \(t\)-test does.
• The bootstrapped confidence interval test does not make assumptions on the performance distribution and estimates empirically the confidence interval \(CI_1\) at level \(\alpha\).
• Selecting a test with a significance level \(\alpha\) enforces a type-I error \(\alpha\) when the assumptions of the test are verified.

The theory: power analysis for the choice of the sample size

We saw that \(\alpha\) was enforced by the choice of the significance level in the test implementation. The second type of error \(\beta\) must now be estimated. \(\beta\) is the probability to fail to reject \(H_0\) when \(H_a\) is true. When the effect size \(\epsilon\) and the probability of type-I error \(\alpha\) are kept constant, \(\beta\) is a function of the sample size \(N\). Choosing \(N\) so as to meet requirements on \(\beta\) is called statistical power analysis. It answers the question: what sample size do I need to have \(1-\beta\) chance to detect an effect size \(\epsilon\), using a test with significance level \(\alpha\)? The next paragraphs present guidelines to choose \(N\) in the context of a Welch’s \(t\)-test.

As we saw above, \(\beta\) can be analytically computed as:

where \(CDF_{H_0}\) is the cumulative distribution function of a \(t\)-distribution centered on \(0\), \(t_\alpha\) is the critical value for significance level \(\alpha\) and \(t_\epsilon\) is the \(t\)-value corresponding to an effect size \(\epsilon\). In the end, \(\beta\) depends on \(\alpha\), \(\epsilon\), (\(s_1\), \(s_2\)) the empirical standard deviations computed on two samples \((x_1,x_2)\) and the sample size \(N\).

Example 2 To illustrate, we compare two DDPG variants: one with action perturbations (\(Algo 1\)) [Lillicrap et al., 2015], the other with parameter perturbations (\(Algo 2\)) [Plappert et al., 2017]. Both algorithms are evaluated in the Half-Cheetah environment from the OpenAI Gym framework.

Step 1 - Running a pilot study

To compute \(\beta\), we need estimates of the standard deviations of the two algorithms (\(s_1, s_2\)). In this step, the algorithms are run in the environment to gather two samples \(x_1\) and \(x_2\) of size \(n\). From there, we can compute the empirical means \((\overline{x}_1, \overline{x}_2)\) and standard deviations \((s_1, s_2)\).

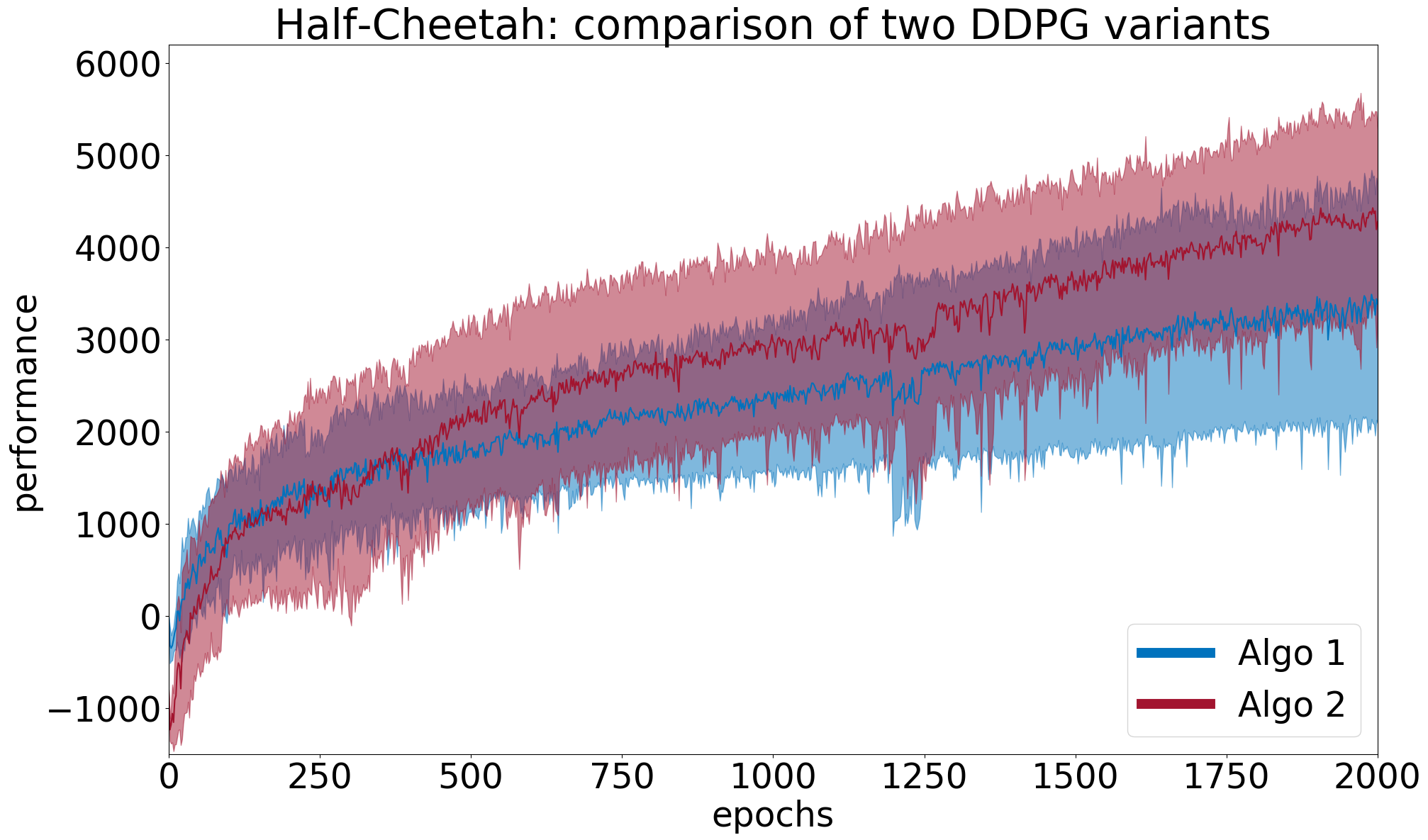
Example 2 (continued) Here we run both algorithms with \(n=5\). We find empirical means \((\overline{x}_1, \overline{x}_2) = (3523, 4905)\) and empirical standard deviations \((s_1, s_2) = (1341, 990)\) for \(Algo1\) (blue) and \(Algo2\) (red) respectively. From Figure 4, it seems there is a slight difference in the mean performances \(\overline{x}_{\text{diff}} =\overline{x}_2-\overline{x}_1 >0\). Running preliminary statistical tests at level \(\alpha=0.05\) lead to a \(p\)-value of \(0.1\) for the Welch’s \(t\)-test, and a bootstrapped confidence interval of \(CI_1=[795, 2692]\) for the value of \(\overline{x}_{\text{diff}} = 1382\). The Welch’s \(t\)-test does not reject \(H_0\) (\(p\)-value \(>\alpha\)) but the bootstrap test does (\(0\not\in CI_1\)). One should compute \(\beta\) to estimate the chance that the Welch’s \(t\)-test missed an underlying performance difference (type-II error).

_{Figure 4: DDPG with action perturbation versus DDPG with parameter perturbation tested in Half-Cheetah. Mean and 95% confidence interval computed over 5 seeds are reported. The figure shows a small difference in the empirical mean performances.}

Step 2 - Choosing the sample size

Given a statistical test (Welch’s \(t\)-test), a significance level \(\alpha\) (e.g. \(\alpha=0.05\)) and empirical estimations of the standard deviations of \(Algo1\) and \(Algo2\) (\(s_1,s_2\)), one can compute \(\beta\) as a function of the sample size \(N\) and the effect size \(\epsilon\) one wants to be able to detect.

Example 2 (continued) For \(N\) in \([2,50]\) and \(\epsilon\) in \([0.1,..,1]\times\overline{x}_1\), we compute \(t_\alpha\) and \(\nu\) using the formulas given in Section \ref{sec:ttest}, as well as \(t_{\epsilon}\) for each \(\epsilon\). Finally, we compute the corresponding probability of type-II error \(\beta\) using Equation~\ref{eq:beta}. Figure 5 shows the evolution of \(\beta\) as a function of \(N\) for the different \(\epsilon\). Considering the semi-dashed black line for \(\epsilon=\overline{x}_{\text{diff}}=1382\), we find \(\beta=0.51\) for \(N=5\): there is \(51\%\) chance of making a type-II error when trying to detect an effect \(\epsilon=1382\). To meet the requirement \(\beta=0.2\), \(N\) should be increased to \(N=10\) (\(\beta=0.19\)).

_{Figure 5: Evolution of the probability of type-II error as a function of the sample size N for various effect sizes epsilon, when (s1, s2)= (1341, 990) and alpha=0.05. The requirement 0.2 is represented by the horizontal dashed black line.}

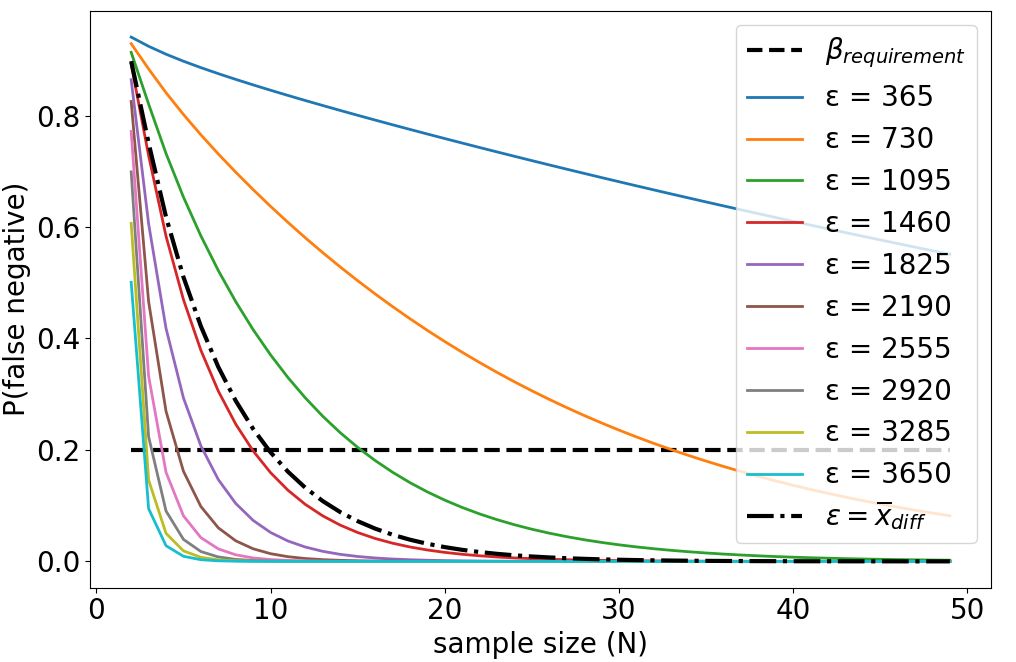
In our example, we find that \(N=10\) was enough to be able to detect an effect size \(\epsilon=1382\) with a Welch’s \(t\)-test, using significance level \(\alpha\) and using empirical estimations \((s_1, s_2) = (1341, 990)\). However, let us keep in mind that these computations use various approximations (\(\nu, s_1, s_2\)) and make assumptions about the shape of the \(t\)-values distribution.

Step 3 - Running the statistical tests

Both algorithms should be run so as to obtain a sample \(x_{\text{diff}}\) of size \(N\). The statistical tests can be applied.

Example 2 (continued) Here, we take \(N=10\) and run both the Welch’s \(t\)-test and the bootstrap test. We now find empirical means \((\overline{x}_1, \overline{x}_2) = (3690, 5323)\) and empirical standard deviations \((s_1, s_2) = (1086, 1454)\) for \(Algo1\) and \(Algo2\) respectively. Both tests rejected \(H_0\), with a \(p\)-value of \(0.0037\) for the Welch’s \(t\)-test and a confidence interval for the difference \(\mu_{\text{diff}} \in [732,2612]\) for the bootstrap test. Both tests passed. In Figure 7, plots for \(N=5\) and \(N=10\) can be compared. With a larger number of seeds, the difference that was not found significant with \(N=5\) is now more clearly visible. With a larger number of seeds, the estimate \(\overline{x}_{\text{diff}}\) is more robust, more evidence is available to support the claim that \(Algo2\) outperforms \(Algo1\), which translates to tighter confidence intervals represented in the figures. \end{myex}

_{Figure 7: Performance of DDPG with action perturbation (Algo1) and parameter perturbation (Algo2) with N=5 seeds (left) and N=10 seeds (right). The 95% confidence intervals on the right are smaller, because more evidence is available (N larger). The underlying difference appears when N grows.}

Important: Given a sample size \(N\), a minimum effect size to detect \(\epsilon\) and a requirement on type-I error \(\alpha\) the probability of type-II error \(\beta\) can be computed. This computation relies on the assumptions of the \(t\)-test. The sample size \(N\) should be chosen so as to meet the requirements on \(\beta\).

In practice: influence of deviations from assumptions

Under their respective assumptions, the \(t\)-test and bootstrap test enforce the probability of type-I error to the selected significance level \(\alpha\). These assumptions should be carefully checked, if one wants to report the probability of errors accurately. First, we propose to compute an empirical evaluation of the type-I error based on experimental data, and show that: 1) the bootstrap test is sensitive to small sample sizes; 2) the \(t\)-test might slightly under-evaluate the type-I error for non-normal data. Second, we show that inaccuracies in the estimation of the empirical standard deviations \(s_1\) and \(s_2\) due to low sample size might lead to large errors in the computation of \(\beta\), which in turn leads to under-estimate the sample size required for the experiment.

Empirical estimation of the type-I error

Remember, type-I errors occur when the null hypothesis (\(H_0\)) is rejected in favor of the alternative hypothesis \((H_a)\), \(H_0\) being correct. Given the sample size \(N\), the probability of type-I error can be estimated as follows:

• Run twice this number of trials (\(2 \times N\)) for a given algorithm. This ensures that \(H_0\) is true because all measurements come from the same distribution.
• Get average performance over two randomly drawn splits of size \(N\). Consider both splits as samples coming from two different algorithms.
• Test for the difference of both fictive algorithms and record the outcome.
• Repeat this procedure \(T\) times (e.g. \(T=1000\))
• Compute the proportion of time \(H_0\) was rejected. This is the empirical evaluation of \(\alpha\).

Example 3 We use \(Algo1\) from Example 2. From \(42\) available measures of performance, the above procedure is run for \(N\) in \([2,21]\). Figure 8 presents the results. For small values of \(N\), empirical estimations of the false positive rate are much larger than the supposedly enforced value \(\alpha=0.05\).

_{Figure 8: Empirical estimations of the false positive rate on experimental data (Example 3) when N varies, using the Welch's t-test (blue) and the bootstrap confidence interval test (orange).}

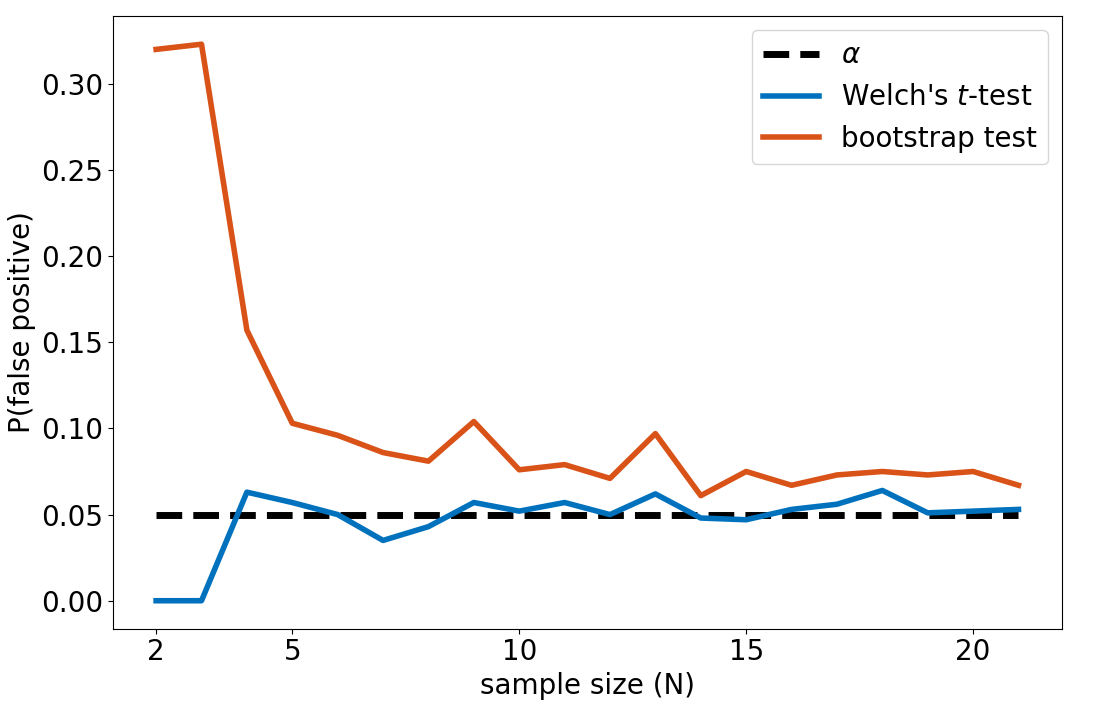
In our experiment, the bootstrap confidence interval test should not be used with small sample sizes (\(<10\)). Even in this case, the probability of type-I error (\(\approx10\%\)) is under-evaluated by the test (\(5\%\)). The Welch’s \(t\)-test controls for this effect, because the test is much harder to pass when \(N\) is small (due to the increase of \(t_\alpha\)). However, the true (empirical) false positive rate might still be slightly under-evaluated. In this case, we might want to set the significance level to \(\alpha<0.05\) to make sure the true positive rate stays below \(0.05\). In the bootstrap test, the error is due to the inability of small samples to correctly represent the underlying distribution, which impairs the enforcement of the false positive rate to the significance level \(\alpha\). Concerning the Welch’s \(t\)-test, this might be due to the non-normality of our data (whose histogram seems to reveal a bimodal distribution). In Example 1, we used \(N=5\) and encountered a type-I error. We can see on the Figure 8 that the probability of this to happen was around \(10\%\) for the bootstrap test and above \(5\%\) for the Welch’s \(t\)-test.

Influence of the empirical standard deviations

The Welch’s \(t\)-test computes \(t\)-statistics and the degree of freedom \(\nu\) based on the sample size \(N\) and the empirical estimations of standard deviations \(s_1\) and \(s_2\). When \(N\) is low, estimations \(s_1\) and \(s_2\) under-estimate the true standard deviation in average. Under-estimating \((s_1,s_2)\) leads to smaller \(\nu\) and lower \(t_\alpha\), which in turn leads to lower estimations of \(\beta\). Finally, finding lower \(\beta\) leads to the selection of smaller sample size \(N\) to meet \(\beta\) requirements. We found this had a significant effect on the computation of \(N\). Figure 9 shows \(\beta\) the false negative rate when trying to detect effects of size \(\epsilon\) between two normal distributions \(\mathcal{N}(3,1)\) and \(\mathcal{N}(3+\epsilon,1)\). The only difference between both figures is that the left one uses the true values of \(\sigma_1, \sigma_2\) to compute \(\beta\), whereas the right figure uses (inaccurate) empirical evaluations \(s_1,s_2\) to compute \(\beta\). We can see that the estimation of standard deviations influences the computation of \(\beta\), and the subsequent choice of an appropriate sample size \(N\) to meet requirements on \(\beta\). See our paper for further details.

_{Figure 9: Evolution of the probability of type-II error as a function of the sample size N and the effect size epsilon, when (s1, s2)= (1-error, 1-error) and alpha=0.05. Left: error=0, this is the ideal case. Right: error=0.40, a large error that can be made when evaluating s over n=5 samples. The compared distributions are normal, one is centered on 3, the other on 3+\epsilon.}

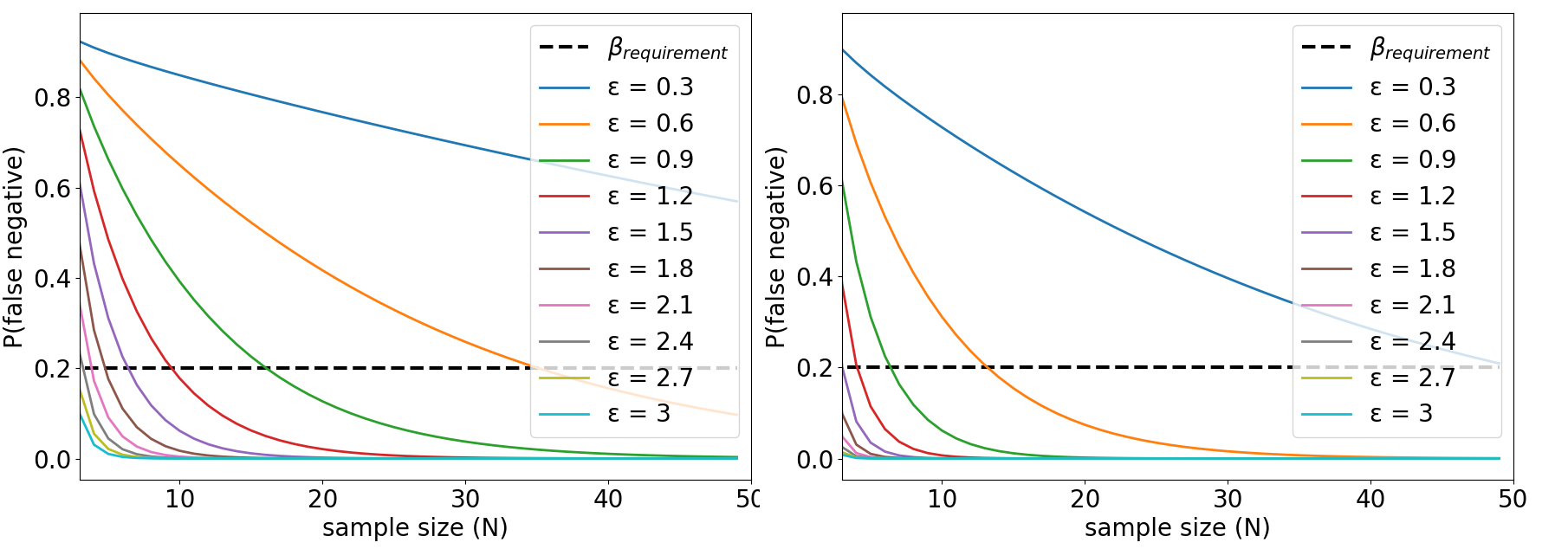
Important:

• One should not blindly believe in statistical tests results. These tests are based on assumptions that are not always reasonable.
• \(\alpha\) must be empirically estimated, as the statistical tests might underestimate it, because of wrong assumptions about the underlying distributions or because of the small sample size.
• The bootstrap test evaluation of type-I error is strongly dependent on the sample size. A bootstrap test should not be used with less than \(20\) samples.
• The inaccuracies in the estimation of the standard deviations of the algorithms (\(s_1,s_2\)), due to small sample sizes \(n\) in the preliminary study, lead to under-estimate the sample size \(N\) required to meet requirements in type-II errors.

Conclusion

In this post, I detailed the statistical problem of comparing the performance of two RL algorithms. I defined type-I and type-II errors and proposed ad-hoc statistical tests to test for performance difference. Finally, I detailed how to pick the right number of random seeds (your sample size) so as to reach the requirements in terms of type-I and II errors and illustrated the process with a practical example.

The most important part is what came after. We challenged the hypotheses made by the Welch’s \(t\)-test and the bootstrap test and found several problems. First, we showed significant difference between empirical estimations of the false positive rate in our experiment and the theoretical values supposedly enforced by both tests. As a result, the bootstrap test should not be used with less than \(N=20\) samples and tighter significance level should be used to enforce a reasonable false positive rate (\(<0.05\)). Second, we show that the estimation of the sample size \(N\) required to meet requirements in type-II error were strongly dependent on the accuracy of (\(s_1,s_2\)). To compensate the under-estimation of \(N\), \(N\) should be chosen systematically larger than what the power analysis prescribes.

Final recommendations

• Use the Welch’s \(t\)-test over the bootstrap confidence interval test.
• Set the significance level of a test to lower values (\(\alpha<0.05\)) so as to make sure the probability of type-I error (empirical \(\alpha\)) keeps below \(0.05\).
• Correct for multiple comparisons in order to avoid the linear growth of false positive with the number of experiments.
• Use at least \(n=20\) samples in the pilot study to compute robust estimates of the standard deviations of both algorithms.
• Use larger sample size \(N\) than the one prescribed by the power analysis. This helps compensating for potential inaccuracies in the estimations of the standard deviations of the algorithms and reduces the probability of type-II errors.

Note that I am not a statistician. If you spot any approximation or mistake in the text above, please feel free to report corrections or clarifications.

References

• Henderson, P., Islam, R., Bachman, P., Pineau, J., Precup, D., & Meger, D. (2017). Deep Reinforcement Learning that Matters. link

• Mnih, V.; Badia, A. P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; and Kavukcuoglu, K. 2016. Asynchronous methods for deep reinforcement learning. In International Conference on Machine Learning, 1928–1937. link

• Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; and Klimov, O. 2017. Proximal policy optimization algorithms. link

• Duan, Y.; Chen, X.; Houthooft, R.; Schulman, J.; and Abbeel, P. 2016. Benchmarking deep reinforcement learning for continuous control. In Proceedings of the 33rd International Conference on Machine Learning (ICML). link

• Gu, S.; Lillicrap, T.; Ghahramani, Z.; Turner, R. E.; Schölkopf, B.; and Levine, S. 2017. Interpolated policy gradient: Merging on-policy and off-policy gradient estimation for deep reinforcement learning. link

• Lillicrap, T. P.; Hunt, J. J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; andWierstra, D. 2015. Continuous control with deep reinforcement learning. link

• Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; and Moritz, P. 2015a. Trust region policy optimization. In Proceedings of the 32nd International Conference on Machine Learning (ICML). link

• Wu, Y.; Mansimov, E.; Liao, S.; Grosse, R.; and Ba, J. 2017. Scalable trust-region method for deep reinforcement learning using kronecker-factored approximation. link

• Plappert, M., Houthooft, R., Dhariwal, P., Sidor, S., Chen, R. Y., Chen, X., … & Andrychowicz, M. (2017). Parameter space noise for exploration. link

Code

The code is available on Github here.

Paper

The paper can be found on ArXiv here.

Contact

Email: cedric.colas@inria.fr

Subscribe to our Twitter.